La época de exámenes es algo curioso, de repente todo lo trivial se vuelve interesante: la trayectoria de las moscas, cualquier cosa que uno se pueda encontrar en la Wikipedia...

En estas me hallaba yo ayer, así que tirando de clásicos acabe "enfrentándome" al problema de P contra NP, y para mi sorpresa creo que di con algo interesante (bueno, eso o entendí algo mal, que es lo más probable :P).

Pero no adelantemos acontecimientos, resulta que escojí un problema NP-completo, satisfacción booleana, y me lié a tirar código, este es el resultado (perdón por la escasez de comentarios):

bool_solve.py: Este es el algoritmo en sí.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
#!/usr/bin/env python
#coding: utf-8

from random import randint
from copy import copy

OR_OP  = 1
AND_OP = 2
NOT_OP = 3

class Operand:
    name = ""
    inverted = False

    def __eq__(self, other):
        return self.__hash__() == other.__hash__()

    def __hash__(self):
        return self.__repr__().__hash__()

    def __init__(self, name, inverted = False):
        assert(not name.startswith('!'))
        self.name = name
        self.inverted = inverted
        self._hash = randint(0, 4294967295)


    def invert(self):
        self.inverted = not self.inverted

    def __str__(self):
        if self.inverted:
            return "!" + self.name
        else:
            return self.name

    def __repr__(self):
        return self.__str__()

# --------------------------------------------
# AND operation functions
# --------------------------------------------

# v is possible under cond ?
def is_acceptable(v, cond):
    if type(cond) == list:
        return all(map(lambda x: is_acceptable(v, x), cond))

    elif type(cond) == set:
        return all(map(lambda x: is_acceptable(v, x), cond))

    else:
        return v.name != cond.name or v.inverted == cond.inverted

# (ow = one way) are src conditions possible under dst ?
def is_ow_acceptable(src, dst):
    if type(src) == list:
        return all(map(lambda x: is_ow_acceptable(x, dst), src))

    elif type(src) == set:
        return all(map(lambda x: is_ow_acceptable(x, dst), src))

    else:
        return is_acceptable(src, dst)

# (tw = two way) are c1 and c2 possible simultaneously
def is_tw_acceptable(c1, c2):
    if c1 == None or c2 == None:
        return False

    ac2 = is_ow_acceptable(c1, c2)
    ac1 = is_ow_acceptable(c2, c1)
    return ac1 and ac2

# --------------------------------------------
# Common operation functions
# --------------------------------------------

# considers the different branches and may output a more compact one
# TODO: actually code the important part :P
def clean_branch_list(bl):
    l = []
    for i in xrange(len(bl)):
        bi = bl[i]

        already_contained = False
        to_delete = []

        le = len(l)
        for j in xrange(len(l)):
            bj = l[j]

            if bi.issubset(bj):
                if len(bj - bi) > 0: # Superset
                    to_delete.append(j)
                else:
                    already_contained = True

            elif bi.issuperset(bj):
                already_contained = True

        if not already_contained:
            l.append(bi)

        offset = 0
        for d in to_delete:
            l.pop(d - offset)
            offset += 1

    return l

# outputs the (con1 or con2) branch list
def rewrite_constraints_or(con1, con2):

    if type(con1) == set:
        con1 = [con1]

    if type(con2) == set:
        con2 = [con2]

    # Null operands?
    if con1 == None:
        if con2 == None:
            return None
        return con2

    elif con2 == None:
        return con1

    return clean_branch_list(con1 + con2)


# outputs the (con1 and con2) branch list
def rewrite_constraints_and(c1, c2):
    if type(c1) == set:
        c1 = [c1]
    elif c1 == None:
        c1 = []

    if type(c2) == set:
        c2 = [c2]
    elif c2 == None:
        c2 = []

    sets = []

    # Some optimization would be great here!! :P
    for x in c1:
        for y in c2:
             if is_tw_acceptable(x, y):
                sets.append(x | y)

    if len(sets) == 0:
        return None
    else:
        return clean_branch_list(sets)


# Obtains recursively the solution branches of a operation
def get_solutions(operand, inverted = False):
    if type(operand) == str:
        op = Operand(operand)
        if inverted:
            op.invert()
        return [set([op])]

    assert(type(operand) == tuple)

    if len(operand) == 2:
        op, op1 = operand
        sol = get_solutions(op1, not inverted)

        if op == NOT_OP:
            return sol
        raise Exception("%i operand doesn't apply to two operands" % op)

    else:
        op, op1, op2 = operand
        sol1 = get_solutions(op1, inverted)
        sol2 = get_solutions(op2, inverted)

        if not inverted:
            if   op == OR_OP:
                return rewrite_constraints_or(sol1, sol2)

            elif op == AND_OP:
                return rewrite_constraints_and(sol1, sol2)

        else:
            if   op == OR_OP:
                return rewrite_constraints_and(sol1, sol2)

            elif op == AND_OP:
                return rewrite_constraints_or(sol1, sol2)


        raise Exception("%i operand doesn't apply to two operands" % op)

# TODO: Update this part
def get_solution_string(s):
    if type(s) == list:
        return ', '.join(map(get_solution_string, s))

    elif type(s) == set:
        return ', '.join(map(get_solution_string, s))

    else:
        return str(s)

# Pretty prints the solution branches
def print_solutions(sols):
    if sols == None:
        print "It's impossible!"
        return

    for s in sols:
        print get_solution_string(s)

    print '%i solution(s)' % len(sols)

bool_test.py: Prueba el código anterior con un ejemplo, y después hace una prueba de tiempos.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
#!/usr/bin/env python
#coding: utf-8

from bool_solve import *
from string import lowercase
from random import randint
from time import time

TEST_VARIABLE_NUMBER = 5
TEST_NUMBER = 20
BATCH_NUMBER = 1

plot_file = "plot.dat"

# Examples
# ========

# Operation = (Op_Code, Operand1, Operand2) | (Op_Code, Operand)
# Operand   = '"' <Operand name> '"' | Operation

# A and (B or ((!B or !C) and (C and (!B and ((!A or D) or B)))
#
#   B (1)       !D (0)
#  /           /
# A -> !B -> C -> D (1)
#         \
#          !C (0)
#
# !A (0)
#
# Results:
#
# A, B
# A, !B, C, D
#

# Negated
# -------

# !(A and (B or ((!B or !C) and (C and (!B and ((!A or D) or B))))
#
# !A (1)
#
#    B (0)     !D (1)
#   /         /
# A -> !B -> C -> D (0)
#        \
#         !C (1)
#
# Results
#
# !A
#  A, !B, !C
#  A, !B,  C, !D
#

op = (AND_OP, 'a', # A and
             (OR_OP, 'b', #  ( B or
                    (AND_OP, # ( x and y )
                             (OR_OP, (NOT_OP, 'b'),  # x = ( !B or
                                     (NOT_OP, 'c')), #       !C  )

                             (AND_OP, 'c' ,                   # y = ( C and
                                      (AND_OP, (NOT_OP, 'b'), #      ( !B and
                                               (AND_OP, 'c',  #       !C ))

                                                        (OR_OP, # ( x or y )
                                                                (OR_OP, (NOT_OP, 'a'), # x = (!A or
                                                                        'd'),           #       D )
                                                                'b'  # y = B ))
                                                        )
                                               )
                                      )
                             )
                    )
             )
     )
# Hey! it looks like lisp, let's try to run it xD

test_variables = set(['a', 'b', 'c', 'd'])

forward_solutions = [set([Operand('a'), Operand('b')]),
                     set([Operand('a'), Operand('b', True), Operand('c'), Operand('d')])]

reverse_solutions = [set([Operand('a', True )]),
                     set([Operand('b', True), Operand('c', True )]),
                     set([Operand('a', False), Operand('b', True), Operand('d', True)])]


def check_solutions(sol1, sol2):
    for i in sol1:
        if not i in sol2:
            raise Exception('Calculation error!')

    for j in sol2:
        if not j in sol1:
            raise Exception('Calculation error!')


# Generates a random boolean table
def make_bool_tree(height, variable_num):
    if height == 0:
        x = randint(0, 1)
        if x == 0:
            return lowercase[randint(0, variable_num - 1)]
        else:
            return (NOT_OP, lowercase[randint(0, variable_num - 1)])

    op = randint(1, 2)
    return (op, make_bool_tree(height - 1, variable_num), make_bool_tree(height - 1, variable_num))

def print_time_table(trees):
    i = 1
    l = []
    for tree in trees:
        t = time()
        solutions = get_solutions(tree)
        t2 = time()

        l.append(t2 - t)
        if solutions != None:
            print "%i: %s [%s solution(s)]" % (i, t2 - t, len(solutions))

        else:
            print "%i: %s impossible" % (i, t2 - t)

        i += 1
    return l

# A simple test
if __name__ == "__main__":

    print "Testing correctness..."
    print '"Forward"'
    solutions = get_solutions(op)
    print_solutions(solutions)
    check_solutions(solutions, forward_solutions)
    print "OK"

    print '\n"Reverse"'
    solutions_n = get_solutions((NOT_OP, op))
    print_solutions(solutions_n)
    check_solutions(solutions_n, reverse_solutions)
    print "OK"

    print "\n\nTesting times..."
    times = []
    for i in xrange(BATCH_NUMBER):
        print "Batch %i of %i" % (i + 1, BATCH_NUMBER)
        trees = map(lambda x: make_bool_tree(x, TEST_VARIABLE_NUMBER), xrange(TEST_NUMBER))
        times.append(print_time_table(trees))

    if plot_file != None:
        f = open(plot_file, 'wt')
        means = []
        for i in xrange(len(times[0])):
            means.append(sum(map(lambda x: x[i], times)) / float(len(times)))

        i = 1
        for m in means:
            print >> f, i, m
            i += 1

Si se lanza el bool_test.py hace sus pruebas y genera un archivo "plot.dat" con los datos de los tiempos, pasados por el Gnuplot sale esto:

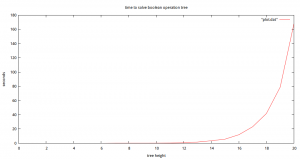
curva exponencial de libro

Y ahi quedo el tema... eso sí, quedé medio mosca por que no entendía como un algoritmo que solo pasa una vez por cada elemento podía generar tiempos tan claramente exponenciales pero en fin...

Esta mañana me di cuenta de por que era así, el problema era que lo que crecía exponencialmente no era el algoritmo, sinó los árboles que se generan para las pruebas, al ser binarios completos el número de nodos es 2^altura, así que reinterpretando los datos...

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
input = "plot.dat"
output = "plot_number.dat"
fin = open(input, "rt")
f = open(output, "wt")

for x in fin.read().split("\n"):
    if len(x.strip()) > 0:
        height, time = x.split(" ", 2)
        print >>f, (1<<(int(height) - 1)), time

f.close()
fin.close()

Sale algo hermosamente lineal:

En resumen, hay distintas posibilidades:

  • La pifié interpretando el problema, y eso no es lo que se supone que había que hacer.
  • La pifié en el código y el ejemplo funciona por pura casualidad. (Creo que esto es lo más probable, realmente no se por que demonios funciona :P)