Es curioso, hay momentos en los que uno tiene que buscar una solución a un problema sencillo, por ejemplo, dadas varias listas de elementos, buscar la más parecida a otra nueva, y encontrar una solución (muy simple!). Pero esta solución no aparece en ningún otro sitio, a alguien se le tuvo que ocurrir! será tan simple (y tan inferior a otras), que no merece la pena documentarla?, simplemente uno no es capaz de encontrarla?... es probable :P...

Después de hacer alguna prueba más... resulta que no escala bien, y con grandes datos pierde ventaja rápidamente xD

Bueno, siendo como fuere, ahí va un algoritmo para buscar la lista (o listas), mas cercana a una dada, sin tener que comparar todos los elementos de todas.

La utilidad es bastante directa, en el campo de la IA (Inteligencia Artificial) hay una serie de algoritmos para hacer clasificación, dado un conjunto de entrenamiento etiquetado (con cada elemento asignado a una categoría) encuentra al conjunto al que pertenece un nuevo elemento.

El acercamiento simplista

Uno de estos algoritmos de clasificación es el KNN (K-Nearest Neighbours, los K vecinos más cercanos). El algoritmo es bastante simple, tenemos una lista de elementos con N características, por ejemplo, la longitud y anchura de el śepalo y pétalo de una serie de flores, y asociado el tipo de flor que es, para saber de que tipo es una nueva flor (conociendo estas 4 características), podemos computar su distancia al resto (como la suma de las diferencias de cada característica).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def distance(element1, element2):
    '''Compute the distance between two elements.'''
    distance_sum = 0

    for dimension in range(len(element1['features'])):
        feature1 = element1['features'][dimension]
        feature2 = element2['features'][dimension]
        distance_sum += pow(feature1 - feature2, 2)

    return distance_sum

Sabiendo las distancias, podemos tomar los K elementos más cercanos y entre ellos escoger la "etiqueta" más común.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
def get_more_represented(near_elements):
    '''Get the label found in more elements.'''
    # Group by label
    counts = {}
    for element in near_elements:
        label = element['label']
        if label not in counts:
            counts[label] = 0

        counts[label] += 1

    # Find the one with more elements
    max_count = 0
    max_label = None
    for label in counts:
        count = counts[label]
        if count > max_count:
            max_count = count
            max_label = label

    return max_label

El número que será K se define por ensayo y error, aunque suele ser uno pequeño como 3 podría ser cualquiera.

Para encontrar los valores mas próximos entonces hay que evaluar la distancia desde el punto a clasificar a todos los ejemplos, y ordenarlos según este criterio. El problema, claro, es que el numero de cálculos para cada dato que se quiera clasificar es proporcional al (número de puntos * número de dimensiones, o características)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
def naive_knn(training, target, k=1):
    '''Classify an element based on training data.

    :param training: The training set.
    :param target: The element to classify.
    '''

    # Compute all distances
    distances = []
    for element in training:
        distances.append((element, distance(element, target)))

    # Sort by distance
    distances = [element for element, dist
                 in sorted(distances, key=lambda x: x[1])]

    # Return the more represented
    return get_more_represented(distances[:k])

Podemos probar el algoritmo contra este dataset. Después de descomprimirlo lo primero será cargarlo:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def to_element(parts):
    '''Convert the comma separated fields into an element.'''
    return {'features': [float(part.strip()) for part in parts[:-1]],
            'label': parts[-1]}


def load(fname='iris.dat'):
    '''Load the Iris dataset from a CSV file.'''
    with open(fname) as f:
        lines = f.read().strip().split("\n")
        return [to_element(line.split(','))
                for line in lines if not line.startswith('@')]

Después tendremos que encontrar una forma de evaluarlo. Una simple y útil es one-out, consiste en lo siguiente: cogemos los datos etiquetados de los que disponemos y por cada uno, lo intentamos clasificar utilizando el resto de la lista. De esta forma sabremos como de bien se hubiera clasificado ese. Cuantos más resultados correctos, mejor, claro.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def one_out(elements, out_index):
    '''Separate one element from the list.

    :param elements: The list of elements.
    :param out_index: The position of the element to extract.
    '''

    if (out_index + 1) >= len(elements):  # Last element is out
        return (elements[:out_index], elements[out_index])
    else:
        return (elements[:out_index] + elements[out_index + 1:],
                elements[out_index])


def naive_knn_cross_validation(elements, k=1):
    '''Simple one-out cross validation.'''
    failed = 0
    for i in range(len(elements)):
        training, out = one_out(elements, i)
        if naive_knn(training, out, k) != out['label']:
            failed += 1

    return failed

Con esto ya podemos ir haciendonos una idea de que tal funciona.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
# Load the training set
elements = load('iris.dat')

# Cross validate each element with the rest of the dataset
failed = naive_knn_cross_validation(elements)

print("Failed {} of {} ({:.3f}%)".format(
    failed, len(elements), (failed * 100) / len(elements)))

# Failed 6 of 150 (4.000%)

De 150 elementos sólo 6 fallan (el 4%). Está bastante bien teniendo en cuenta lo simple e intuitivo del algoritmo, verdad? Veamos entonces la forma de hacer esta búsqueda de elementos más rápida (esto fué sobre 150 elementos en 4 dimensiones, es un caso muy limitado).

El algoritmo

Esta idea surgió intentando que la búsqueda sobre ~8000 elementos con más de 20 dimensiones fuese algo más... ligera ante la preocupación de que hubiera problemas cuando el conjunto de datos siguiera creciendo. Está pensado para evitar tener que comprobar todas las dimensiones de todos los elementos, y aún así garantizar que los elementos son los más cercanos, la idea es bastante simple.

Por ejemplo, supongamos que tenemos 3 elementos en 2 dimensiones, y queremos encontrar el más cercano a un punto (0).

Las distancias en cada dimensión a tres puntos (A, B, C) podrían ser:

1
2
D1: (punto=A, distancia=1), (punto=B, distancia=2), (punto=C, distancia=3)
D2: (punto=B, distancia=1), (punto=C, distancia=2), (punto=A, distancia=3)

Calculamos las distancias en la primera dimensión, y las introducimos en una lista ordenada por la distancia en esa dimensión, junto con el punto al que pertenecen y el número de dimensiones que ha sido computado hasta el momento.

1
(punto=A, dist=1, dim_comp=1), (punto=B, dist=2, dim_comp=1), (punto=C, dist=3, dim_comp=1)

Tomamos el primer punto de la lista (el más cercano hasta ahora)

1
(punto=A, dist=1, dim_comp=1)

Sumamos a la distancia de la primera dimensión la de la segunda (1 + 3) y la introducimos en la lista de acuerdo a la posición que le corresponde por su nueva distancia (sin olvidar cambiar el número de dimensiones computadas).

1
(punto=B, dist=2, dim_comp=1), (punto=C, dist=3, dim_comp=1), (punto=A, dist=4, dim_comp=2)

Repetimos el paso con el siguiente elemento más cercano:

1
(punto=B, dist=2, dim_comp=1)

La nueva distancia será 2 + 1 (la distancia hasta el momento, más el de la siguiente dimensión), así que al añadirlo a la lista se quedará así:

1
(punto=B, dist=3, dim_comp=2), (punto=C, dist=3, dim_comp=1), (punto=A, dist=4, dim_comp=2)

(En este momento tanto el punto B como el C podrían ser el primero, da igual, pero si como desempate se hace que el elemento con más número de dimensiónes quede antes nos podemos ahorrar alguna iteración)

Sacamos de nuevo el primer elemento:

1
(punto=B, dist=3, dim_comp=2)

Y como ya hemos computado todas las dimensiones de este elemento y aún así sigue siendo elmás cercano, no hace falta seguir con el resto de puntos, sabemos seguro que es el más cercano.

Si generalizamos el algoritmo para K vecinos, quedaría algo así:

1. Crear una lista vacía “vecinos”.
2. Calcular la distancia en la primera dimensión de cada elemento hasta el nuevo punto.
3. Organizarlas en una lista de tuplas (distancia, número de dimensiones hasta el momento, punto)
4. Ordenar la lista según la distancia, de forma ascendente
5. Tomar el menor elemento

6. Si se han tomado en cuenta todas las dimensiones para ese punto:
   6.1 Pasarlo a la lista de “vecinos” como el siguiente más cercano.
   6.2 Si la longitud de la lista de vecinos ya es `K`, ya se ha acabado.

7. Si aún queda alguna dimensión:
   7.1 Calcular la nueva distancia sumándole la de la siguiente dimensión a la ya acumulada.
   7.2 Introducir en la lista ordenada de acuerdo a la nueva distancia computada, con el nuevo número de dimensiones.

8. Volver al paso `5`

 

Así de simple, o, en python:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# Allows to maintain a sorted list
from heapq import heappush, heappop

# Make elements sortable (dicts() are not)
class Element:
    def __init__(self, element):
        self.e = element

    def __lt__(self, other):
        return False


def sorted_knn(training, target, k=1):
    '''Classify an element based on training data.

    :param training: The training set.
    :param target: The element to classify.
    '''

    # Compute all distances for the first feature
    distances = []
    num_features = len(target['features'])
    for element in training:

        # Elements are entered in the list in tuples
        # (distance, last_dimension_computed, element)
        heappush(distances,
                 (pow(element['features'][0] - target['features'][0], 2),
                  1,
                  Element(element)))

    nearest = []
    while True:
        # Get the nearest element yet
        distance, next_feature, element = heappop(distances)

        # If all features are computated, it's the next on the nearest list
        if next_feature == num_features:
            nearest.append(element)

            if len(nearest) >= k:
                break

        # Else, add it back to the heap
        else:
            new_distance = distance + pow(element.e['features'][next_feature] -
                                          target['features'][next_feature], 2)
            heappush(distances,
                     (new_distance, next_feature + 1, element))

    # Return the more represented
    return get_more_represented([element.e for element in nearest])

Y eso es todo lo necesario, si repetimos la validación, veremos que el ratio de acierto es el mismo.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
def sorted_knn_cross_validation(elements, k=1):
    '''Simple one-out cross validation.'''
    failed = 0
    for i in range(len(elements)):
        training, out = one_out(elements, i)
        if sorted_knn(training, out, k) != out['label']:
            failed += 1

    return failed

# Cross validate each element with the rest of the dataset
failed = sorted_knn_cross_validation(elements)

print("Failed {} of {} ({:.3f}%)".format(
    failed, len(elements), (failed * 100) / len(elements)))

# Failed 6 of 150 (4.000%)

Pero si comparamos velocidades, para distintas K, vemos que no se comportan igual.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
from time import time

def benchmark(elements,times=100, k=3):
    print("Naive KNN")
    t1 = time()
    for _ in range(times):
        naive_knn_cross_validation(elements=elements, k=k)
    t2 = time()
    t = t2 - t1
    print("{:.3f}s, {:.3f}s/iteration".format(t, t / times))

    print("Sorted KNN")
    t1 = time()
    for _ in range(times):
        sorted_knn_cross_validation(elements=elements, k=k)
    t2 = time()
    t = t2 - t1
    print("{:.3f}s, {:.3f}s/iteration".format(t, t / times))

for k in (1, 3, 5, 7, 9):
    print("K={}".format(k))
    benchmark(elements, k=k)
    print()

# K=1
# Naive KNN
# 9.514s, 0.095s/iteration
# Sorted KNN
# 6.763s, 0.067s/iteration

# K=3
# Naive KNN
# 9.467s, 0.094s/iteration
# Sorted KNN
# 7.837s, 0.078s/iteration

# K=5
# Naive KNN
# 9.472s, 0.094s/iteration
# Sorted KNN
# 8.512s, 0.085s/iteration

# K=7
# Naive KNN
# 9.426s, 0.094s/iteration
# Sorted KNN
# 9.094s, 0.090s/iteration

# K=9
# Naive KNN
# 9.481s, 0.094s/iteration
# Sorted KNN
# 9.809s, 0.098s/iteration

En resumen, que al principio mantener la lista ordenada es más eficiente, pero a medida que aumenta la K, se pierde la ventaja y se empieza a notar el coste de O(log N) por inserción (en vez de uno constante en una lista normal) que implica mantener la lista ordenada.

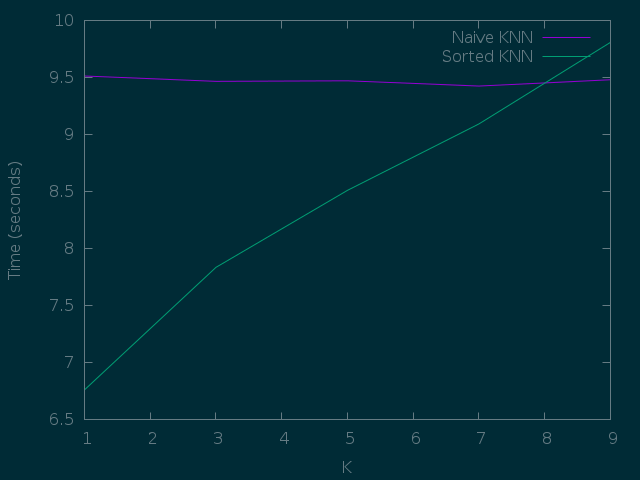
Así que como curiosidad está bien, pero para cosas reales parece que no :P